
Introduction d’un logiciel de simulation d’algorithmes dans le processus enseignement-apprentissage de l’algorithmique chez les apprenants débutants de l’ENSET de Libreville
Médard-Sylvain Ovono sylvain_ovono@hotmail.com Jean-François Hérold jean-françois.herold@univ-amu.fr Jacques Ginestié jacques.ginestie@univ-amu.fr
Résumé
Cet article qui présente notre projet de thèse est une première approche visant à faire la présentation d’une tentative d’introduction des TICE, en l’occurrence une application de simulation d’algorithmes (Algobox) dans le processus enseignement- apprentissage de l’algorithmique chez des apprenants débutants. L’utilisation de ce logiciel a pour objectif de proposer une contribution au problème du fort taux d’échec constaté par les responsables administratifs et pédagogiques depuis plusieurs années dans l’enseignement de l’algorithmique à l’ENSET de Libreville.
Mots clés
Algorithmique, simulation, enseignement-apprentissage, logiciel
Introduction
L’enseignement de la programmation est prescrit à l’École normale supérieure de l’enseignement technique (ENSET) de Libreville au Gabon depuis sa création par l’ordonnance 81/72. Cet enseignement est dispensé aux élèves professeurs de première année dans toutes les options par le biais de deux modules de trente
heures. Le premier module est une initiation à l’algorithmique, le second module étant consacré à l’apprentissage d’un langage de programmation.
Depuis plusieurs années, et en dépit des efforts conjugués des enseignants et des apprenants, on constate un fort taux d’échec dans ces deux modules. Au regard de ce manque de réussite chez les apprenants, on est en droit de se poser la question de savoir quelles sont les raisons de ces échecs.
C’est donc pour tenter de cerner les causes de ces échecs et d’y proposer des solutions que nous avons entrepris ce travail de thèse.
Cette communication porte sur notre projet de thèse, à travers lequel nous nous proposons de comprendre les raisons qui font que les apprenants ont de mauvais résultats dans l’enseignement-apprentissage de l’algorithmique et des langages informatiques tel qu’il se fait actuellement à l’ENSET de Libreville. Après avoir fait l’analyse de la manière dont le cours est actuellement dispensé, nous envisagerons une autre approche de la mise en œuvre de ce processus d’enseignement-apprentissage de l’algorithmique avec l’utilisation d’un outil informatique d’aide à l’élaboration des algorithmes.
Objet de la recherche
La question liée au problème de l’échec des apprenants dans le processus enseignement-apprentissage de l’algorithmique, voire des langages informatiques, interpelle à plus d’un titre tout didacticien des sciences et/ou de la technologie dans un établissement de formation de formateurs de l’enseignement technique. En effet, l’enseignement-apprentissage de l’algorithmique et des langages informatiques, comme celui des mathématiques et de la physique est considéré comme un enseignement transversal indispensable à une meilleure compréhension des disciplines technologiques que le futur professeur doit enseigner, mais aussi à un bon usage des TICE dans ses pratiques pédagogiques.
Cette question de l’échec dans l’enseignement de l’algorithmique et des langages informatiques est préoccupante pour les principaux responsables administratifs et pédagogiques de notre établissement, l’ENSET de Libreville. On observe, en effet, sur les trois dernières années, un pourcentage d’échec de 88 % en moyenne, comme le montre le tableau 1 ci-dessous. Des remédiations ont été proposées par les responsables de cette école. C’est ainsi que le module consacré à l’algorithmique et à la programmation d’une durée de quarante-cinq heures a finalement été découpé en deux modules de trente heures chacun : l’un consacré à l’algorithmique et l’autre à la programmation. La principale raison évoquée pour expliquer les mauvais résultats des étudiants était que les apprenants étaient totalement novices dans ce domaine et n’avaient pas assez de temps pour tirer profit de cet enseignement.
Tableau 1 : Pourcentage d’échec des trois dernières années
| Année | Taux d’échec (%) |
| 2012 | 93,2 |
| 2013 | 86, 3 |
| 2014 |
84,5 |
En fait, traditionnellement, l’enseignement de l’algorithmique et/ou d’un langage informatique s’appuie sur des problèmes à résoudre. L’enseignement- apprentissage de l’algorithmique et des langages informatiques impliquent alors chez l’apprenant deux activités cognitives : l’apprentissage du formalisme de l’algorithmique, puis d’un langage informatique, et une démarche de résolution de problème. Aussi, l’apprenant est amené, d’une part, à apprendre le formalisme de l’algorithmique, puis celui du langage informatique ; et, d’autre part, à résoudre le problème de la tâche prescrite. Cette double activité cognitive ne facilite pas chez les apprenants l’apprentissage en raison de la charge cognitive générée par cette double activité (Amadieu et Tricot, 2006).
Il nous faut donc nous interroger sur l’enseignement-apprentissage de l’algorithmique et des langages informatiques tel qu’il est actuellement effectué à l’ENSET de Libreville : comment et pourquoi sont-ils enseignés ; quelle est la place de l’algorithmique et des langages informatiques dans le curriculum de formation des élèves professeurs de l’ENSET de Libreville ; quels sont les savoirs induits par cet enseignement, si ces savoirs sont transposables et comment ; comprendre de quelle manière le processus enseignement-apprentissage se met en œuvre dans de telles situations ; et enfin, envisager l’élaboration de nouvelles approches pour permettre la construction d’une pédagogique adaptée (Ginestié, 2008).
Dans cette perspective, le recours à l’utilisation d’un intermédiaire graphique (TICE) permet d’envisager une réduction possible de la charge cognitive pour améliorer les apprentissages des élèves, comme l’utilisation d’un logiciel d’aide à l’élaboration et à l’exécution d’algorithmes (AlgoBox 1), cette utilisation se faisant selon les prescriptions liées à l’usage de l’ordinateur comme média d’enseignement (Depover, 1987 ; Brandt-Pomares et Boilevin, 2008), dans le cadre d’une animation développant une pédagogie constructiviste (Denis, 1993).
Dans les pays africains en général, et à l’ENSET de Libreville au Gabon en particulier, en raison de sa gratuité, ce type de logiciels est très utilisé par les enseignants qui souhaitent intégrer les TICE dans leurs pratiques pédagogiques. En effet, ces pays manquent de ressources et les enseignants ne sont pas ou très peu outillés dans les classes pour une utilisation des TICE. En outre, dans le contexte de l’ENSET de Libreville, la quasi-totalité des élèves professeurs sont des bacheliers technologiques (F, MI) ; ils n’ont donc pas fait d’initiation à l’algorithmique dans leur programme de formation au lycée.
1. AlgoBox est un logiciel libre et gratuit d’aide à l’élaboration et à l’exécution d’algorithmes. Doté d’une interface en français, claire et ergonomique, il est d’une prise en main facile et rapide. (Téléchargeable à partir du lien suivant : http://www.cndp.fr/sialle/fiche-detaillee-algobox-482.php).
Éléments de problématique
L’apprentissage de l’algorithmique et des langages informatiques convoque au moins deux champs théoriques qui interfèrent dans l’analyse des processus d’enseignement-apprentissage : l’un, relevant de la didactique des sciences et/ ou de la technologie, l’autre, relevant de la psychologie des apprentissages. On s’intéressera aussi à l’usage de l’ordinateur dans l’enseignement (technologies de l’information et de la communication pour l’enseignement, ou TICE), en discutant d’un certain nombre de questions sur l’apprentissage de l’algorithmique et des langages informatiques, en liaison aux instruments informatiques (Bruillard, 2001 ; 2006 ; 2013).
Knuth (1981) définit l’algorithmique comme étant un ensemble fini de règles qui donne une suite d’opérations afin de résoudre un type spécifique de problème. Kitajima (2004) précise la définition de Knuth (1981) en indiquant qu’un algorithme est un ensemble d’opérations nécessaires pour la résolution d’un problème en décrivant les étapes qui permettent d’atteindre le résultat. En d’autres termes, un algorithme est une suite finie et non ambiguë d’instructions permettant de donner la réponse à un problème.
À travers ces définitions, l’algorithme apparaît comme étant une procédure permettant de résoudre un problème posé, mais qui s’appuie sur un formalisme spécifique (description des opérations nécessaires, procéduralisation). De ce fait, dans l’apprentissage de l’algorithmique, deux activités apparaissent: l’apprentissage des règles syntaxiques (apprentissage du formalisme) et donner la réponse à un problème (la résolution du problème).
Cette double activité dans le processus enseignement-apprentissage de l’algorithmique, voire des langages informatiques, suggère deux activités qui peuvent être concurrentes. Il est donc nécessaire de se demander si c’est l’apprentissage des règles syntaxiques et/ou le processus d’analyse du problème à résoudre qui met les apprenants en situation d’échec. Ce, d’autant, que Sweller (1988) met en évidence le fait que les processus cognitifs qui sont impliqués dans la résolution d’un problème sont différents de ceux qui sont impliqués dans l’acquisition de connaissances. En effet, selon D’Hainaut (2000), la résolution de problèmes implique des structures de connaissances nouvelles au niveau de la situation, et met en jeu des concepts et des opérations appris antérieurement mais qui sont mis en œuvre d’une nouvelle manière. Pour Richard (2005), résoudre un problème nécessite d’avoir les connaissances propres au contexte spécifique de la situation-problème, de produire des raisonnements nécessaires afin de pouvoir identifier les actions possibles et de les ordonner. L’élaboration de ce processus de résolution aux problèmes posés peut donc être coûteux cognitivement pour un élève en situation d’apprentissage (Tricot, 2003). En effet, un problème peut être facile pour un apprenant qui dispose des connaissances appropriées et peut s’avérer être très difficile pour un apprenant ne disposant pas de ces connaissances, ou si le contexte spécifique de la situation-problème ne ressemble à rien de connu pour l’apprenant (Cauzimille-Marmèche, 1991 ; 1996).
Questions de recherche envisagées
Nous faisons l’hypothèse qu’en introduisant dans le processus d’enseignement- apprentissage un logiciel de simulation d’algorithmes, comme « AlgoBox », le système cognitif de l’apprenant sera soulagé, en partie, de l’activité liée à l’apprentissage du formalisme de l’algorithme. Plus de ressources cognitives pourront alors être consacrées à l’analyse et à la compréhension du problème, donc à sa résolution. Le simulateur, en facilitant l’activité d’apprentissage du formalisme, pourrait réduire la charge cognitive de l’apprenant (Paas et van Merriënboer, 1994 ; Sweller, 2010), facilitant ainsi l’apprentissage.
On envisage également une étude similaire sur l’apprentissage d’un langage informatique.
De plus, on s’interrogera également sur les savoirs qui sont réellement mis en œuvre dans de telles situations (apprentissage de l’algorithmique voire d’un langage informatique), et on s’interrogera sur comment ces savoirs peuvent être transposés dans une situation didactique correspondant aux disciplines visées (automatique, informatique industrielle, automate programmable industriel, etc.). Ce questionnement se fera à travers l’analyse de l’activité d’apprenants à partir, entre autres, des propositions de Bastien (1997) sur la fonctionnalisation des connaissances et leur contextualisation.
Présentation d’Algobox
Très utilisé dans l’enseignement des mathématiques en séries scientifiques dans les lycées en France, Algobox est, selon ses développeurs, un logiciel d’initiation à l’algorithmique. Au lancement, on distingue deux zones de texte : présentation de l’algorithme et code de l’algorithme (figure 1). La première zone est un en-tête qui permet de dire ce que fait l’algorithme, tandis que la seconde permet de saisir le pseudo-code de la déclaration des variables et du corps de l’algorithme. Une série de boutons et d’onglets permettent l’insertion, la modification et la suppression d’objets.
Figure 1 : Écran d’accueil
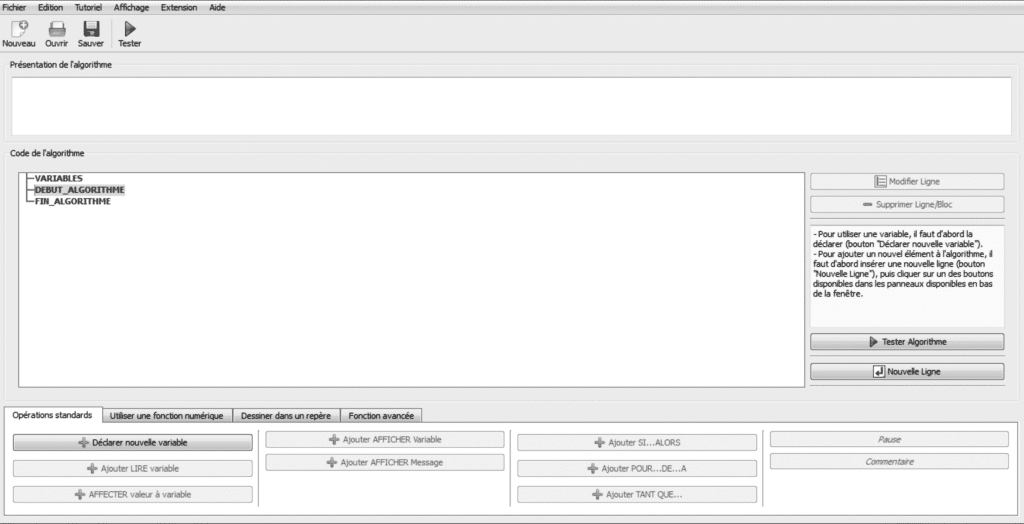
Figure 1 : Écran d’accueil
Après le lancement de l’interface d’accueil, les instructions de l’algorithme sont construites à partir d’un mini-langage algorithmique de type « pseudo-code ». À l’exception des fonctions mathématiques, toutes les instructions sont en français. Des instructions de base que l’on insère en cliquant sur les boutons de l’interface permettent de construire progressivement et de façon hiérarchique et structurée l’algorithme. Ceci permet à l’utilisateur de se concentrer sur l’élaboration de l’algorithme et ainsi de s’affranchir des difficultés liées à son formalisme (figure 2).
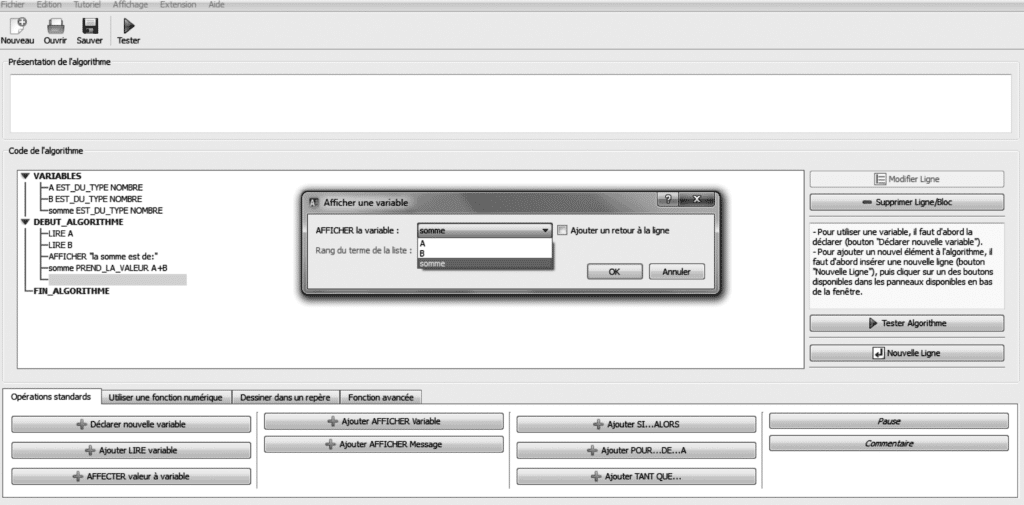
Figure 2 : Afficher une variable
Lors de l’édition d’algorithmes plus complexes, un mode « éditeur de texte » permet aux utilisateurs avancés de taper directement les instructions de l’algorithme à l’aide d’un éditeur incorporé muni de certaines fonctions permettant de faciliter la saisie et la compréhension de l’algorithme.
Après cette édition, l’exécution de l’algorithme élaboré se fait grâce à un bouton « tester l’algorithme » (figure 3). Il existe également un bouton qui permet l’exécution de l’algorithme ligne par ligne afin d’observer le résultat de chaque ligne du programme. Cette exécution s’appelle le mode « pas à pas pédagogique ».
Après cette édition, l’exécution de l’algorithme élaboré se fait grâce à un bouton « tester l’algorithme » (figure 3). Il existe également un bouton qui permet l’exécution de l’algorithme ligne par ligne afin d’observer le résultat de chaque ligne du programme. Cette exécution s’appelle le mode « pas à pas pédagogique ».
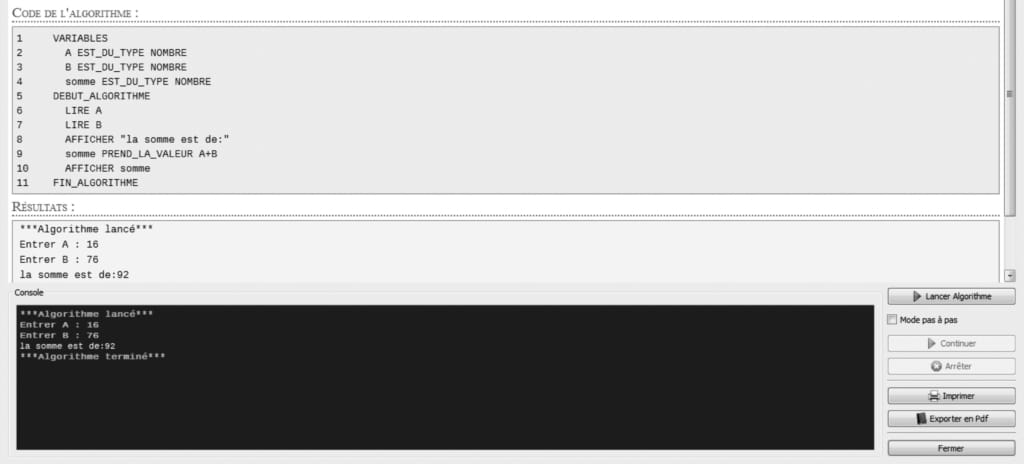
Figure 3 : Fenêtre d’exécution d’Algobox
Au regard de la simplicité d’utilisation de cette application, Algobox dispenserait effectivement l’apprenant d’une grande partie des tâches liées à l’apprentissage du formalisme syntaxique de l’algorithmique. Il offre, en effet, à l’apprenant la possibilité de rentrer le pseudo-code soit en cliquant sur des boutons, soit par le biais de propositions prédéfinies.
En revanche, l’utilisation de ces propositions de pseudo-code nécessite cependant la connaissance des structures d’un algorithme, des fonctions prédéfinies et d’un vocabulaire spécialisé même si celui-ci ne présente aucune barrière linguistique car étant en français. Eu égard à ces observations, on se pose alors la question de savoir si ce logiciel peut servir d’outil dans le processus enseignement-apprentissage de l’algorithmique à l’ENSET, outil qui pourrait favoriser l’apprentissage des apprenants.
Le cours d’algorithmique
Dans l’organisation pédagogique actuelle de l’ENSET, le cours d’algorithmique, désigné dans les maquettes des enseignements par « Informatique 2 », est donné au semestre 2. C’est un module de trente heures réparties en vingt heures de cours magistral et dix heures de travaux dirigés (TD). Il représente trois crédits. L’objectif général de ce module est de permettre aux apprenants de maîtriser les notions de base de l’algorithmique afin de permettre à ces derniers d’écrire des algorithmes, puis in fine, les préparer à étudier la programmation (langage informatique ou/et langage d’automate programmable industriel).
Actuellement, des séquences pédagogiques sous la forme de TD sont organisées après l’examen en cours de chacune des notions qui le constitue. Les étudiants, après la recherche de la solution, proposent volontairement au tableau leur production. Celle-ci est selon le cas, proposée comme corrigée type si elle est correcte, ou discutée et toilettée (c’est-à-dire qu’on y retire toutes les erreurs) si elle est incorrecte avant d’en faire une correction pour l’ensemble des apprenants. En introduisant dans cette organisation le logiciel d’aide à l’élaboration d’algorithme Algobox, on peut envisager le même module de trente heures avec quinze heures de cours magistral pour présenter le langage de description d’algorithmes (LDA), une séance de cinq heures pour présenter l’application, enfin
dix heures de travaux pratiques (TP) compléteront le dispositif.
Après la découverte des premières notions importantes qui nécessiteront l’organisation de TP, l’enseignant devra en s’appuyantsur un petitexercice (évaluation formative) présenter le logiciel. Puis par la suite, comme dans l’ancien dispositif, des séances de TP d’élaboration d’algorithme avec Algobox compléterontle cours magistral. Pour les évaluations sommatives (notes de classe et examens de synthèse), les étudiants auront à résoudre des problèmes directement en encodant l’algorithme
sur l’application et en le simulant correctement.
Exemple d’activité proposée actuellement aux étudiants
Actuellement, dans une séquence d’enseignement, les étudiants, après le cours magistral, participent à des séances de travaux dirigés (TD).
Nous présentons ci-dessous un exemple type d’énoncé d’exercice proposé aux étudiants lors de ces séances de TD :
« Écrire un algorithme qui affiche la racine carrée de tous les entiers allant de 1 jusqu’à 10. »
Au cours de la séance de TD, et après avoir examiné leurs propositions de solution, c’est-à-dire qu’une ou plusieurs solutions sont mises au tableau et discutées par les étudiants avec l’enseignant afin d’en extraire un corrigé type. Celui-ci est proposé aux étudiants :
programme RACINEPOUR
variables RACINE : réel n : entier début
pour n de 1 à 10 faire
RACINE • sqrt(n)
écrire (RACINE)
fpour
fin
À travers cet exemple d’activité proposée aux étudiants, on peut faire le constat qu’entre ce qui est demandé par la tâche prescrite et le résultat attendu, le cheminement peut être long et fastidieux pour un étudiant novice en algorithmique. En effet, la réalisation de la tâche prescrite par l’étudiant impose des connaissances, des raisonnements qui seront éventuellement à l’origine d’une surcharge cognitive suivant le niveau d’apprentissage de l’étudiant.
Exemple d’activité possible avec Algobox
Saisie de la solution envisagée dans Algobox
Dans une situation pédagogique avec Algobox, on demanderait aux étudiants d’utiliser l’application pour saisir la solution envisagée. On aurait la proposition suivante :

Figure 4 : Saisie de l’algorithme avec Algobox
Simulation de la solution envisagée
Après la saisie de la solution, la proposition d’algorithme est simulée sur l’interface d’Algobox. On observerait le résultat suivant :
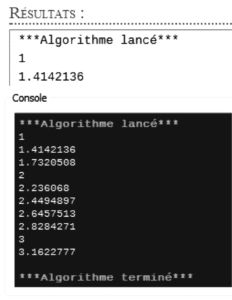
Figure 5 : Résultat de la simulation
Discussion
Au regard de cette activité, nous pouvons la décomposer en trois étapes.
Dans la première étape, on analyse l’énoncé du problème et on repère les mots clés censés orienter vers le choix de la solution, comme :
- « Affiche » : utilisation d’une instruction d’écriture (affichage du résultat) ;
- « Racine carrée » : utilisation d’une assignation (affectation) pour effectuer un calcul, ici la racine carrée ;
- « Entiers » : utilisation d’une variable entière ;
- « Allant de 1 jusqu’à 10 » : utilisation d’une structure itérative.
Il est donc nécessaire que l’apprenant soit en mesure d’identifier ces mots clés. Pour cela, il doit être capable de bien comprendre l’énoncé (savoir ce qu’on lui demande). Lorsqu’il a compris ce qui lui est demandé, il se pose la question des éléments utiles pour l’élaboration de l’algorithme. C’est à ce moment qu’il doit identifier des indices (« mots clés ») dans l’énoncé pouvant l’aider dans l’élaboration de sa solution. À ce niveau, il est important de constater que la connaissance de la structure de l’algorithme est indispensable car c’est elle qui permettra de choisir un mot comme « mot clé » et ensuite de lui donner un sens (l’instruction algorithmique associée au mot clé).
Après cette première étape de la compréhension de l’énoncé, l’apprenant va produire ce qu’il estime être la réponse attendue au problème qui lui est posé. Pour cela, il va devoir utiliser de façon cohérente tous les éléments de connaissance nécessaires, cohérence imposée par le respect obligatoire de certaines règles, syntaxiques et logiques, de l’écriture d’un algorithme. C’est à ce niveau que l’on peut considérer que l’élaboration de l’algorithme sans outil d’aide comme Algobox devrait être plus coûteuse cognitivement pour l’étudiant novice qu’avec l’utilisation d’Algobox. En effet, avec Algobox, la structure estdirectementvisible sur l’interface, les instructions sont directement accessibles via des boutons, les types sont proposés sur une liste déroulante, etc. Ici, l’apprenant construit sa solution avec des indications syntaxiques et logiques proposées par l’application. Ce qui n’est pas le cas bien évidemment dans une activité sans Algobox.
Au terme de la construction de sa solution, l’apprenant qui utilise Algobox aura la possibilité de voir si sa solution produit le résultat escompté grâce à la simulation, ce qui n’est pas le cas bien sûr si on n’utilise pas l’outil (formalisme papier). Dans le cas d’Algobox, il serait difficile qu’une erreur de type syntaxique soit commise. Cependant, des erreurs logiques peuvent être faites comme la confusion de fonctions logiques.
Conclusion
En conclusion, et à ce niveau de notre travail de recherche, il nous est encore difficile de nous prononcer sur l’efficacité, en termes d’efficacité du processus enseignement-apprentissage, d’un dispositif d’enseignement utilisant un outil comme Algobox. Cependant, nous pouvons déjà mettre en avant, dans tous les cas, que dans un dispositif d’enseignement mis en œuvre s’appuyant sur un outil comme Algobox ou non, il est nécessaire pour l’apprenant de maîtriser les structures algorithmiques et les notions associées à l’élaboration des algorithmes. Il doit surtout bien comprendre l’énoncé, ce qui est, à notre sens, un élément capital pour qu’il puisse produire une solution au problème posé.
Bibliographie
Amadieu et Tricot. (2006). Utilisation d’un hypermédia et apprentissage : deux activités concurrentes ou complémentaires ? Psychologie Française, 51(1), 5-23.
Bastien. (1997). Les connaissances de l’enfant à l’adulte. Paris : Armand Colin. Benedetto. (2013). Psychologie cognitive : concepts fondamentaux. Paris : Studyrama.
Bruillard et Baron. (2006). Usages en milieu scolaire : caractérisation, observation et évaluation. Dans Grandbastien et Labat. (dir.), Environnements informatiques pour l’apprentissage humain (p. 269-284). Paris : Lavoisier.
Baron et Bruillard. (2001). Une didactique de l’informatique ? Revue française de pédagogie (135)135, 163-172.
Brandt-Pomares et Boilevin. (2008). Didactique des sciences physiques, didactique de la technologie et usage des TICE. Journal of e–Learning and knowledge society, 4(2), 245-254.
Cauzimille-Marmèche. (1991). Apprendre à utiliser ses connaissances pour la résolution de problèmes : analogie et transfert. Bulletin de psychologie, 44(399), 156-164.
Cauzimille-Marmèche. (1996). Effet du rôle assigné à l’expert dans la résolution en dyade asymétrique d’une tâche de combinatoire. Archives de psychologie, 64, 109-131.
Depover. (1987). L’ordinateur média d’enseignement, cadre conceptuel, problématique et recherches.
Bruxelles : Éditions De Boeck.
Denis. (1993). Les animateurs développent-ils une pédagogie constructiviste en robotique pédagogique ? Dans Regards sur la robotique pédagogique : actes du 4e colloque international sur la robotique pédagogique. INRP.
D’Hainaut, (2000). Des fins aux objectifs de l’éducation. Bruxelles : Éducation Éditions Labor. Ginestié. (2008). From task to activity: a re-distribution of role between teacher and pupils. Dans
Ginestié (dir.), The cultural transmission of artefacts, skills and knowledge: Eleven studies in technology education (p. 225-257). Rotterdam : Sense Publishers.
Kitajima. (2004). Modèles quantitatifs d’algorithmes parallèles (thèse de doctorat), Institut national polytechnique de Grenoble, Grenoble.
Knuth. (1973). The art of computer programming, volume 2: Seminumerical algorithms (2e edition).
Massachusetts : Addisso-Wesley.
Paas et Van Merriënboer. (1994). Instructional control of cognitive load in the training of complex cognitive tasks. Educational Psychology Review, 6(4), 351-371.
Pastré, Parage, Richard, Sander, Labat, Futtersack. (2009). La résolution de problèmes professionnels sur simulateur. Activités, 6(1), 3-28.
Richard. (2005). Les activités mentales en résolution de problèmes : comprendre, raisonner, trouver une solution. Paris : Armand Colin.
Sweller. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285.
Sweller. (2010). Element interactivity and intrinsic, extraneous, and germane cognitive load.
Educational Psychology Review, 22, 123-138.
Tricot, Plegat-Soutjis, Campus, Amiel, Lutz et Morcillo. (2003). Utilité, utilisabilité, acceptabilité : interpréter les relations entre trois dimensions de l’évaluation des EIAH. Dans C. Desmoulins,
- Marquet et Bouhineau (dir.), Environnement informatique pour l’apprentissage humain
(p. 391-402). Paris : ATIEF/INRP.
Tricot. (2003). Apprentissage et recherche d’information dans des documents électroniques. Mémoire pour l’habilitation à diriger des recherches, université de Toulouse Le Mirail (128 p.).








